The glass phase: a physics mystery

In physics the glass phase is deemed to be a special form of a solid. While the material feels hard, it lacks a regular crystalline structure. Physicists still cannot explain the transition from a liquid to this special solid form. Solving this mystery will bring numerous applications within reach. Fast-working computer chips, for example, or recyclable plastic. The glass phase can even help us better understand asthma and cancer metastasis.

We all learned it in high school: the three best-known states of matter are gas, liquid and solid. A material with the same molecules can switch between these three states and having done so will behave completely differently. The difference lies in the movement of the molecules: as the temperature (or pressure) increases, they become more energetic.

But there is a phase that looks like both a liquid and a solid at the same time: the glass phase. On the outside the material behaves like a solid, but inside it appears as disorderly as a liquid. Nonetheless, as far as physics is concerned, a material in the glass phase is a solid.

Quadrillion times more viscous than water

The temperature triggers the transition from one state to another. As the temperature falls, atoms move less and less until eventually they can do nothing more than vibrate on the spot. When the transition from a liquid to a solid occurs, the atoms can slow down in one of two ways. If each one settles in a permanent spot, regularly spaced from every other atom, we refer to their arrangement as a crystalline lattice and the material as being crystalline. If, by contrast, the molecules are not neatly ordered in a lattice, but remain jumbled together in what we would call a disorderly structure, we say the material is amorphous or is in the glass phase. Oddly enough, this structure still looks the same as the structure of a liquid. Thus something happens during the transition from a liquid to a solid that causes the molecules to remain in disarray.

When we take a look at how easily the material flows and deforms, also called the viscosity, things become even more interesting. The more difficulty atoms have moving, the more viscous the liquid. Water has a viscosity of 1 mPa·s, and so it flows very easily. The atoms can move easily. The viscosity of honey, by contrast, is 10000 mPa·s; the atoms can move less easily with respect to each other. Looking at amorphous solids we find that the viscosity is more than a quadrillion times greater than that of water. How can it be that the structure remains almost the same during the transition from a liquid to an amorphous solid while the viscosity increases by 15 orders of magnitude? To this day this remains a mystery to physicists.

Janssen’s quest

In 2012, the last year of her doctoral research in Nijmegen, Liesbeth Janssen read an article on glass formation. ‘That such an everyday material was so poorly understood intrigued me.’ Janssen then mailed one of the authors of the article, David Reichman of Columbia University in New York. ‘I told him that I wanted to solve the physics mystery of the glass transition, and in that same year I was able to do my first postdoc under his supervision in New York.’

Janssen’s ultimate drive in her postdoc was to write the definitive universal theory of glass. ‘My supervisor told me that it was an impossible task, which only increased my determination.’ Since then, as an Assistant Professor, Janssen has set up her own group  in the Department of Applied Physics at Eindhoven University of Technology. Even now she is still working to fathom the glass transition.

What will having a theory like this enable us to do? A whole lot, just take a look at the applications in the colored panels accompanying this article. For example, Janssen is researching recyclable plastic, computer bits and even asthma, cancer and how wounds heal.

Janssen's aim is to develop a theory that explains how the viscosity of a material can increase so incredibly quickly in the glass phase, while the material's structure remains almost unchanged. This theory must predict where and how the transition to the glass phase occurs based on a single input: the structure of the material.

No assumptions

‘There's no shortage of theories about glass, but none of them is complete,’ says Janssen. A complete theory, she believes, becomes a possibility when you take the established laws of physics as your sole starting point. The 'ab initio' or first principles approach, as it is known. Janssen explains: ‘This method requires that you start by solving a mathematical equation exactly, and without recourse to any approximations or assumptions.’

Given this, during her first postdoc in New York, Janssen took as her starting point an exact mathematical equation, compiled in accordance with Newton's laws. Based on the molecular structure, this equation predicts the increase in viscosity. But there's more work involved; all the terms used in this equation must be defined.

The German physicist Wolfgang Götze was the first person who managed to partly solve this equation for a glass-forming material. In the 1980s, working at the University of Munich, he wrote a theory for this: the Mode Coupling Theory. The theory was promising; he was able to predict a transition from liquid to glass based on what is known as the cage effect. Yet in some respects the theory falls short of reality. In practice, the cage effect turns out to be correct only for the initial stage of glass formation, and what is known as the fragility—an important aspect for functional applications of glass—is not well predicted at all by this theory.

Atoms in a cage

Götze put forward the cage effect as an explanation for the considerable difference in movement between a liquid and an amorphous solid. The cage effect enables the theory to predict how well atoms or molecules can still travel through a material during the transition from liquid to solid. The more viscous the material, thus the closer to the transition to the glass phase, the greater the difficulty the atoms have in moving through the crowd of atoms. They are, as it were, captured in their own cage.

‘This can best be compared with a crowded festival at which you want to walk from the middle of the field to the stage. If it is very crowded, the individuals around you must themselves step aside before you can pass. It is the same with atoms. It is certainly crowded in a liquid, but neighboring atoms can still just about move aside to allow another atom to move to a new position. In a glass it is so crowded that the atoms can no longer change position, they can only wobble a little on the spot,’ Janssen explains.

This cage effect from the Mode Coupling Theory describes the initial stage of the glass formation very well. But closer to the glass transition, deficiencies arise. Specifically, Janssen discovered that it is not only the neighboring atoms that need to be included, ‘because every atom also needs to know precisely where these neighboring atoms are located, and also where their neighbors are, and their neighbors, and so on,’ says Janssen. Physicists refer to this as having correlation effects across several length scales; Janssen has been able to add this to her own theory.

Fragile glass

But that is not the only shortcoming that had to be solved. The Mode Coupling Theory cannot accurately predict the fragility value of materials. Fragility is a term that denotes how abruptly a material transitions from a liquid to an amorphous solid. In some amorphous solids, such as glass as we know it in windows and vases, the transition is rather gradual.

Janssen: ‘In other amorphous solids, by contrast, we see an abrupt transition, whereby the viscosity first increases very slowly before suddenly soaring.’ The more abrupt the transition, the greater the fragility. Thus every material has its own fragility value. But no theory currently exists that can predict the fragility value of a material.

Janssen then wrote her own, more extensive theory named Generalized Mode Coupling Theory. This can predict the fragility based on the structure of the molecules, and it includes an extensive cage effect. Janssen: ‘Unfortunately this mathematical equation contains multiple unknown terms. I have been working to solve these terms since 2012.’  

To solve one such unknown term exactly, Janssen worked out a new equation for it. But that equation in turn revealed another new unknown term. For that term, she again wrote a new equation. And when that new equation again included an unknown term, she again wrote a new equation for it. Which is how hierarchically linked equations are created. And they go on infinitely.

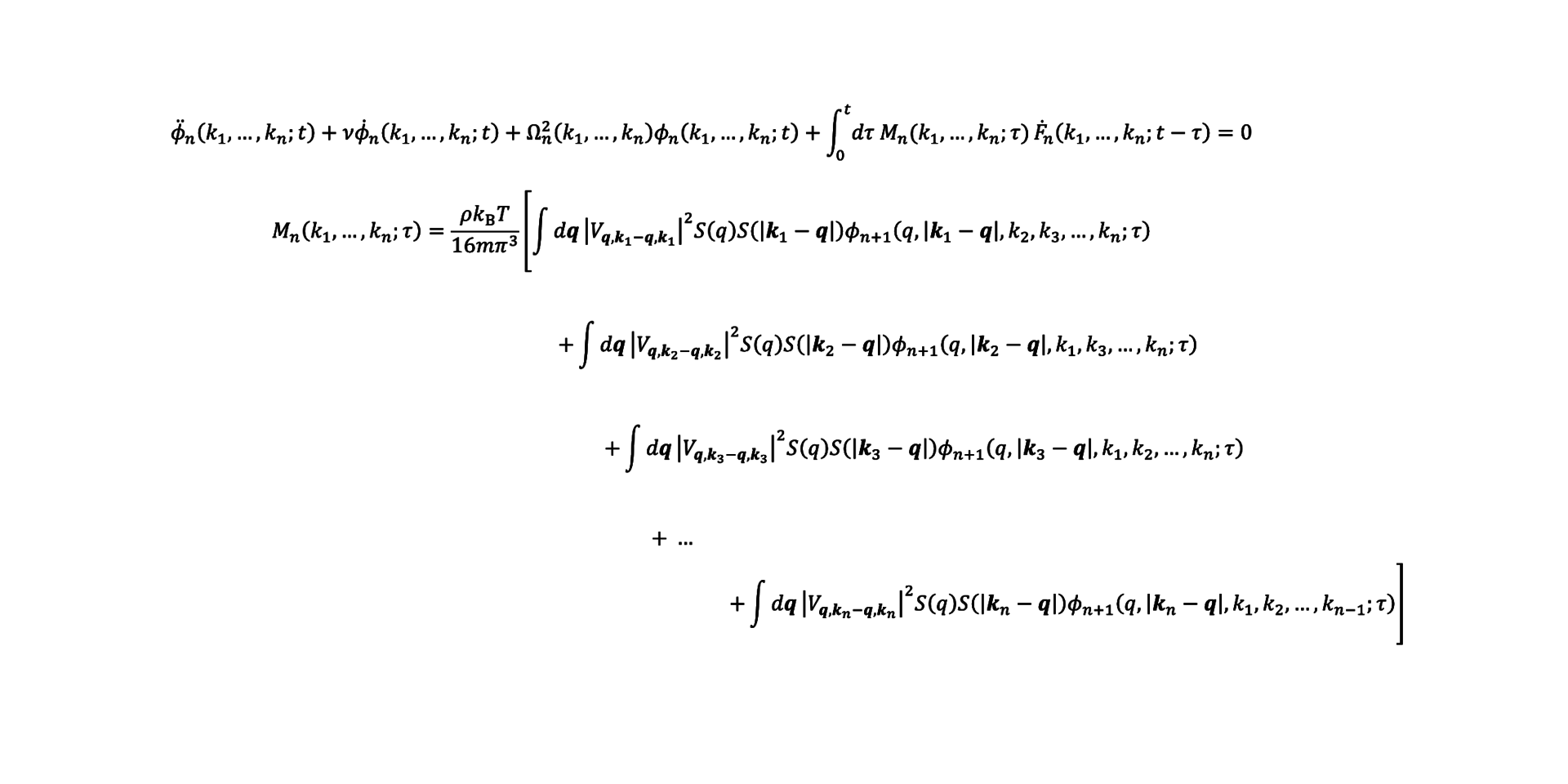
Janssen: ‘For every temperature you have to pull off this stunt yet again, and the closer you get to the glass transition, the more equations you have to include. So you can imagine the kind of computation this requires.’ Janssen and the PhD candidates in her group literally spend hours solving equations with pen and paper. During her postdoc in New York, Janssen got down to five levels of the hierarchy. Her current PhD candidates have continued calculating since then, and have now got down to seven levels.

Next challenge

Now that Janssen has come this far, it is time for the next challenge. The equation above has been written for materials consisting of one type of particle. These particles may be atoms, but could equally be larger building blocks such as colloids—microscopic versions of hard marbles. Physicists use this material as the simplest system for modeling the glass transition.

Janssen is now working on predictions for materials consisting of multiple types of particles. After all, nearly all materials consist of multiple atoms. Take a vase, for example, which consists mainly of silicon and oxygen atoms.

This in itself makes the equation a whole lot more complicated; now you have to start calculating in matrices. To include two types of atoms, you already need a matrix of 2 by 2. Some colloidal glasses require at least 20x20 equations. It's enough to make you want to throw in the towel.

Brute force

Given all this, it seems impossible that the mystery will ever be solved. But Janssen is full of hope. ‘Every week we make modest progress.’ A little while ago, for example, Janssen was at a conference while her two PhD candidates back at the department were trying to solve the first 2x2 matrix equation. ‘They were trying to solve the equations as elegantly as possible, but had hit a brick wall. I advised them to keep on calculating, using brute force. That might well result in an ugly equation, but at least you will have solved it. The next day they told me they had succeeded. And the equations are even elegant!’ tells Janssen proudly.

Nonetheless, the equations are becoming increasingly difficult, and soon it will be almost impossible to do the calculations with pen and paper. Something which Janssen is already anticipating. In 2020 she wants to hire a new postdoc who will focus exclusively on machine learning. Janssen: ‘I want to improve my Generalized Mode Coupling Theory using intelligent brute force, in other words with the help of machine learning techniques. This is an entirely new domain in my field, but has very strong potential. The whole problem of the glass transition is that we can't see any difference between a liquid and a glass in terms of the atomic structure. Machine learning algorithms, on the other hand, are ideally suited to discovering small differences in data that we humans fail to notice. If an algorithm like this can tell us which correlation effects between atoms are the most important, we can use this information to further improve the theory in an efficient manner.’

If Janssen succeeds in developing the definitive theory of glass, she will be realizing a long-held dream in her field of research. ‘The possibilities this will create are truly endless. With applications in diverse fields ranging from the computer sector to the medical world,’ concludes Janssen with eager anticipation.