Time-domain integral equations in electromagnetics

Testing of electronic equipment and systems against the impact of an electromagnetic impulse (EMP) is a standard procedure for military systems. The EMP couples with the circuitry and cables inside the military equipment, causing current surges and eventually breakdown of semiconductors. EMP shielding is focused on preventing component breakdown by locating points of entry.
 

During design of military equipment, guidelines aid the designer in EMP shielding. Still, testing is required to guarantee safety. Although experimental testing is possible for smaller systems, for systems as large as e.g. naval ships this would become very costly. Numerical modelling in combination with small-scale experimental data is a more cost-effective approach, which would aid in developing a more robust shielding design in a full-threat EMP environment.

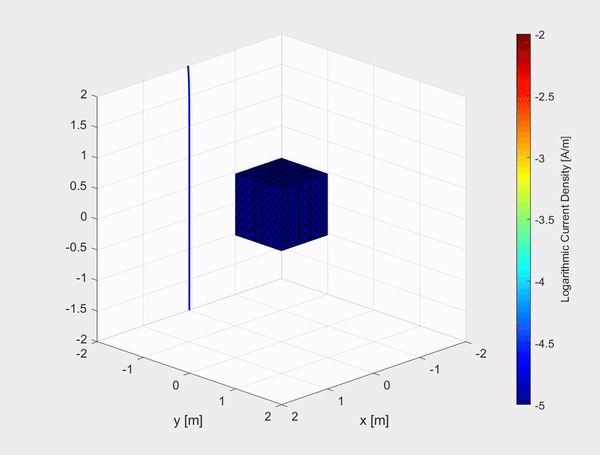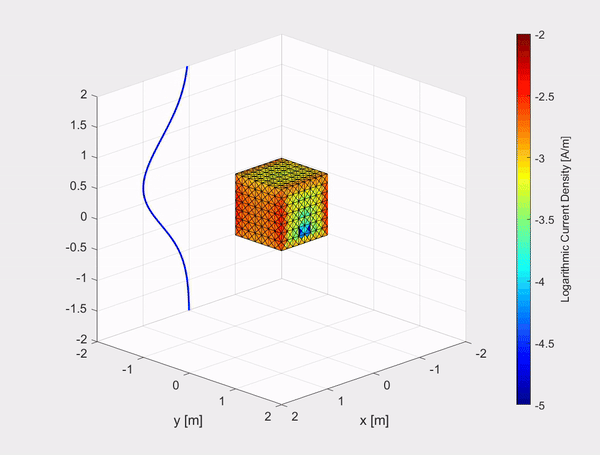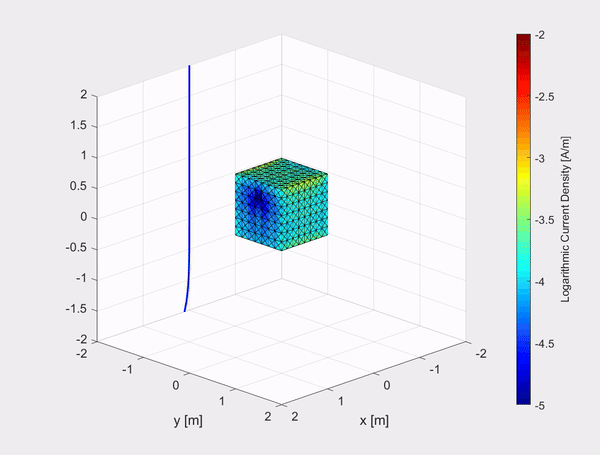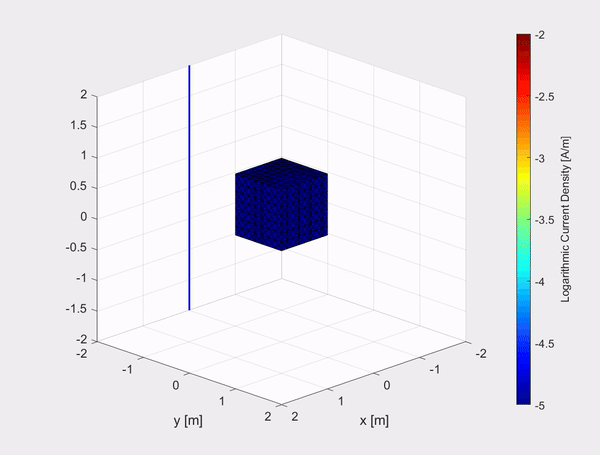
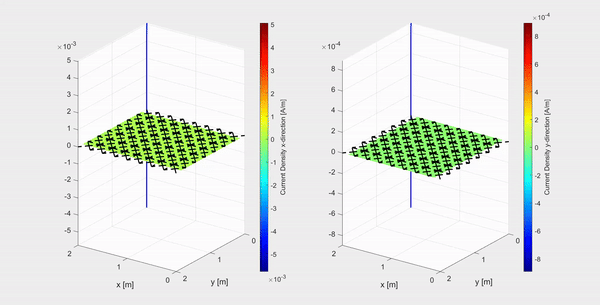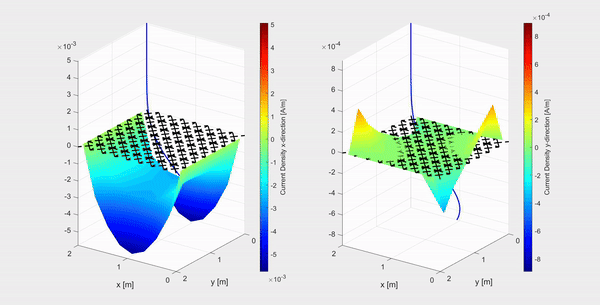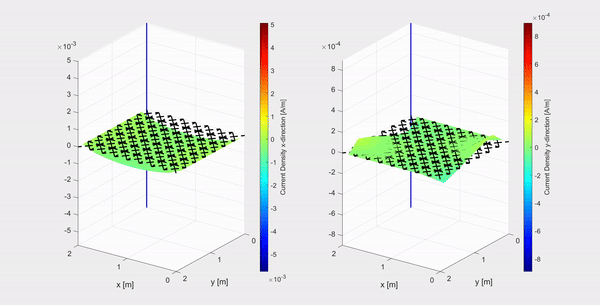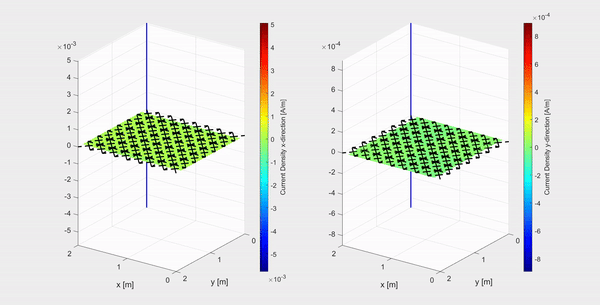
A collaboration between the electronic defense department at TNO and the Electromagnetics group has resulted in an implementation of a numerical method for the time-differentiated electric field integral equation (TD-EFIE), to calculate the equivalent surface current density on a perfect electric conductor (PEC) excited by an incoming pulsed electromagnetic plane wave. In the first clip above an example is shown of an electromagnetic Gaussian plane wave polarized in the x-direction and travelling in the negative z-direction, represented by the evolving blue curve in the (x,z)-plane, hitting a 2 m by 2 m PEC plate. The current density in the x-and y-direction (left and right respectively) are plotted on a logarithmic scale.

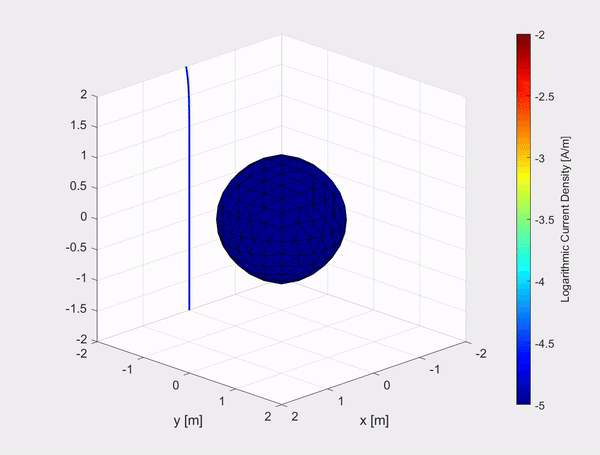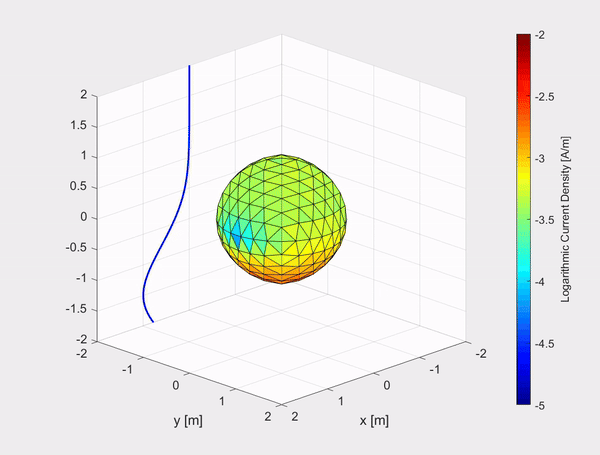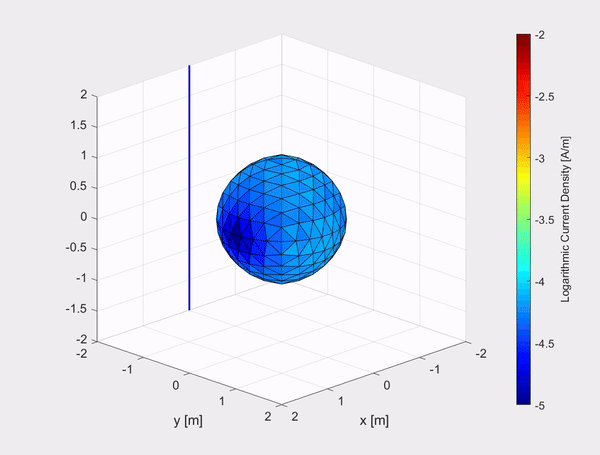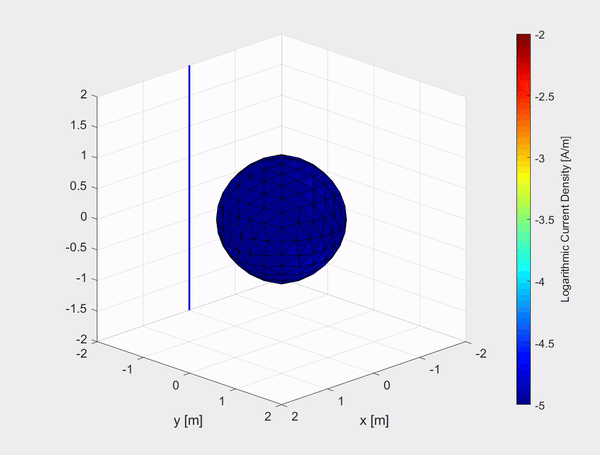
The inhouse built TD-EFIE numerical model has also been tested on other objects such as a 1 m by 1 m by 1 m PEC cube and a sphere with a diameter of 2 m. The movies show the logarithmic current density on the objects due to an incident Gaussian plane polarized in the x-direction and travelling in the negative z-direction, represented by the evolving blue curve in the (x,z)-plane.

Hyperthermia is the localized heating of tissue to improve the effectiveness of cancer treatments like chemotherapy and radiation therapy. The heating can be achieved electromagnetically, where a set of antennas are used to focus the electromagnetic waves to a specific spot inside the body. The propagation of electromagnetic waves through the human body differs per person. Hence, every patient requires hyperthermia treatment planning. The planning consists of an MRI or CT-scan to determine the organ geometry and position, followed by numerical simulations to compute a suitable antenna operation. 

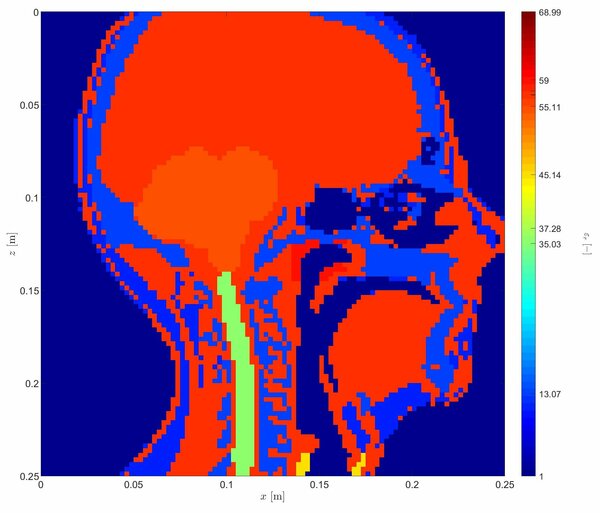
To maximize the effectiveness of hyperthermia, the geometry of the human tissue is extremely important. However, the simulation of small details results in excessive simulation times. Numerical simulations based on time domain integral equations can potentially reduce the simulation time several orders. We have researched these techniques in the past few years and developed a time-domain volume contrast current density integral equation (TDJVIE) solver. The solver can handle the high permittivity values of the human tissue and we illustrate its capabilities in the clip below. A detailed depiction of the relative permittivity of the different tissues found in the sagittal plane of a human head are shown on the right, which is accurate up to 2.5 millimeters.

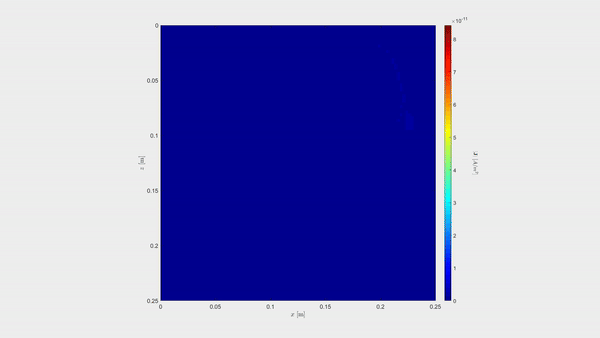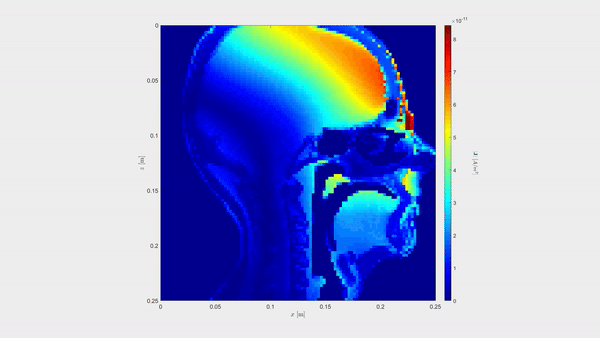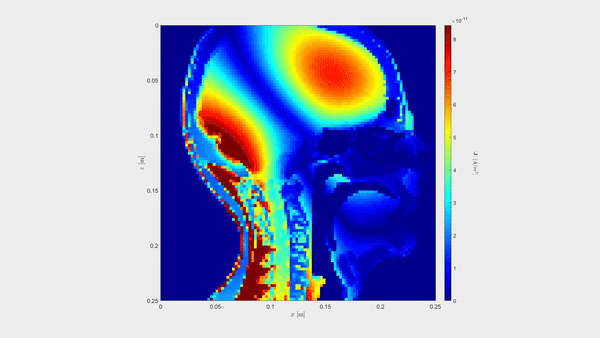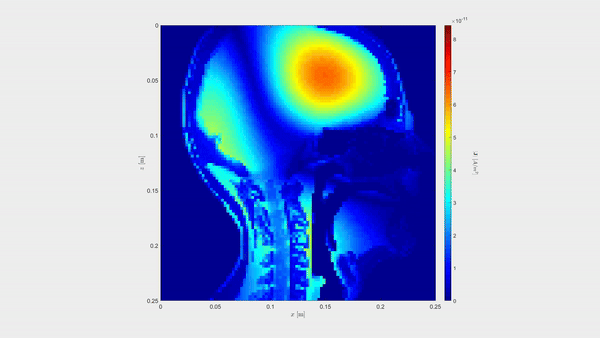
Below that, we show the contrast current density induced by a Gaussian plane wave in the sagittal plane of the head.